2x2 System of Linear Equations Solver
A 2x2 system of linear equations has the form:
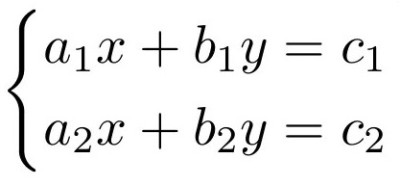
Fill in a1, b1, c1, a2, b2, c2 to proceed with solving a 2x2 system of linear equations
How to solve a 2x2 system of linear equations?
For example, solve the following 2x2 system of linear equations:
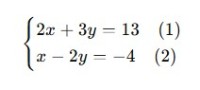
Substitution Method
Express one variable in terms of the other from the second equation:
- x - 2y = -4 → x = 2y - 4
Substitute x = 2y - 4 into the first equation:
- 2(2y - 4) + 3y = 13
- 4y - 8 + 3y = 13
- 7y - 8 = 13 → 7y = 21 → y = 3
Substitute y = 3 into the expression x = 2y - 4:
- x = 2(3) - 4 = 6 - 4 = 2
The solution to the system of equations is: (x, y) = (2, 3)
Algebraic Addition Method
Multiply coefficients to eliminate one variable. Multiply the second equation by 2:
The system of equations becomes:
2x + 3y = 13 and 2x - 4y = -8
Subtract the two equations to eliminate x:
- (2x + 3y) - (2x - 4y) = 13 - (-8)
- 7y = 21 → y = 3
Substitute y = 3 into the equation x - 2y = -4:
- x - 2(3) = -4
- x - 6 = -4 → x = 2
The solution to the system of equations is: (x, y) = (2, 3)