Kalkulator Sistem Persamaan Linear Dua Variabel
Sistem dua variabel memiliki bentuk:
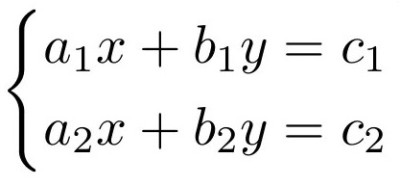
Isi a1, b1, c1, a2, b2, c2 untuk melanjutkan penyelesaian sistem dua variabel (2x2)
Bagaimana Menyelesaikan Sistem Dua Variabel
Contohnya, selesaikan sistem persamaan berikut:
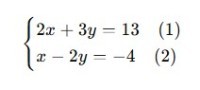
Metode Substitusi
Ungkapkan satu variabel dalam istilah yang lain dari persamaan kedua:
- x - 2y = -4 → x = 2y - 4
Substitusi x = 2y - 4 ke dalam persamaan pertama:
- 2(2y - 4) + 3y = 13
- 4y - 8 + 3y = 13
- 7y - 8 = 13 → 7y = 21 → y = 3
Substitusi y = 3 ke dalam ekspresi x = 2y - 4:
- x = 2(3) - 4 = 6 - 4 = 2
Solusi dari sistem persamaan adalah: (x, y) = (2, 3)
Metode Penambahan Aljabar
Kalikan koefisien untuk menghilangkan satu variabel. Kalikan persamaan kedua dengan 2:
Sistem persamaan menjadi:
2x + 3y = 13 dan 2x - 4y = -8
Kurangi kedua persamaan untuk menghilangkan x:
- (2x + 3y) - (2x - 4y) = 13 - (-8)
- 7y = 21 → y = 3
Substitusi y = 3 ke dalam persamaan x - 2y = -4:
- x - 2(3) = -4
- x - 6 = -4 → x = 2
Solusi dari sistem persamaan adalah: (x, y) = (2, 3)